안녕하세요, 오늘은 퍼셉트론에 대해서 알아보도록 하겠습니다.
퍼셉트론은 여러 개의 input 신호를 받아, 하나의 output 신호를 출력하는 알고리즘입니다. 이는 인공 신경망, 즉 Neural Network을 구성하는 가장 간단한 단위라고 할 수 있습니다.
아래 그림 [1-1]을 보면, 퍼셉트론은 다수의 신호를 받아 하나의 신호를 출력할 수 있습니다. 입력으로 받은 신호에 각각 가중치를 곱한 뒤, 임계값을 초과하면 1을, 아니면 0을 출력합니다.
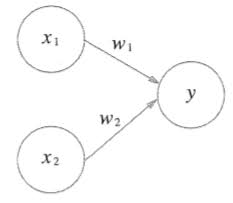
퍼셉트론은 입력으로 받은 신호에 각각 가중치를 곱한 값이, 임계값($\theta$)를 초과하면 1, 임계값 이하이면 0을 출력합니다. 따라서 이는 간단한 형태의 이진 분류기(Binary Classificator)로 볼 수 있습니다.
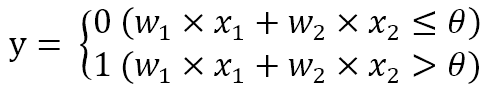
가중치($w_1, w_2, ...$) : 각 입력 신호가 결과에 주는 영향력(중요도)를 조절하는 매개변수
편향($b (-\theta)$) : 뉴런이 얼마나 쉽게 활성화되는지 정하는 매개편수
단순 논리 회로
입력이 두 개인 퍼셉트론으로 우리는 단순 논리 회로를 만들 수 있습니다.

- AND: $(w_1, x_1, θ) == (0.5, 0.5, 0.7)$
- OR: $(w_1, x_1, θ) == (0.5, 0.5, 0.3)$
- NAND: $(w_1, x_1, θ) == (-0.5, -0.5, -0.7)$
NAND는 NOT AND이므로, AND의 가중치에 전부 음수만 붙여 주면 만들 수 있습니다.
퍼셉트론의 한계
위에서 우리는 퍼셉트론을 이용하여 AND, OR, NAND와 같은 3가지 논리 회로를 만들어 보았습니다. 하지만, 결론적으로 XOR은 만들 수 없습니다. 다음 그림을 보며 이유를 설명하겠습니다.
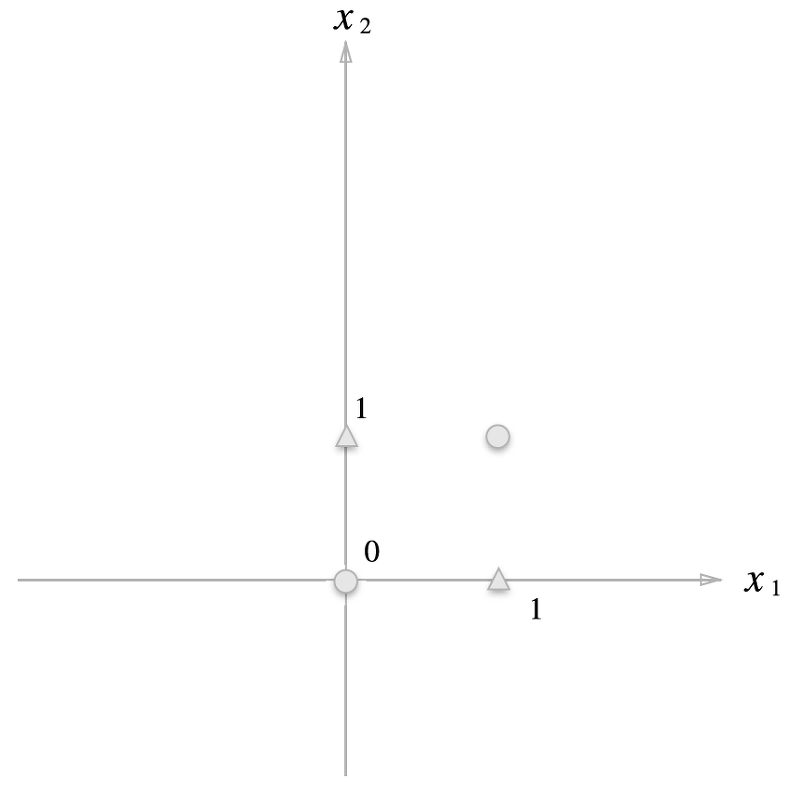
퍼셉트론의 식을 보면, 직선 하나를 그어서 두 가지로 분류하는 선형 이진 분류기라고도 할 수 있습니다. 이는 즉, 선형 영역만 표현할 수 있다는 것입니다.
그러나 XOR은 직선 하나만 그어서는 동그라미와 세모를 나눌 수 없습니다. XOR은 $(0, 0), (1, 1)$의 값은 0, $(1, 0), (0, 1)$ 값은 1이기 때문입니다.
다층 퍼셉트론 (multi-layer perceptron)

다층 퍼셉트론이란 말 그대로 퍼셉트론을 여러 층으로 쌓은 퍼셉트론을 의미합니다. 이렇게 퍼셉트론을 여러 층으로 쌓으면 비선형 영역도 표현할 수 있습니다.
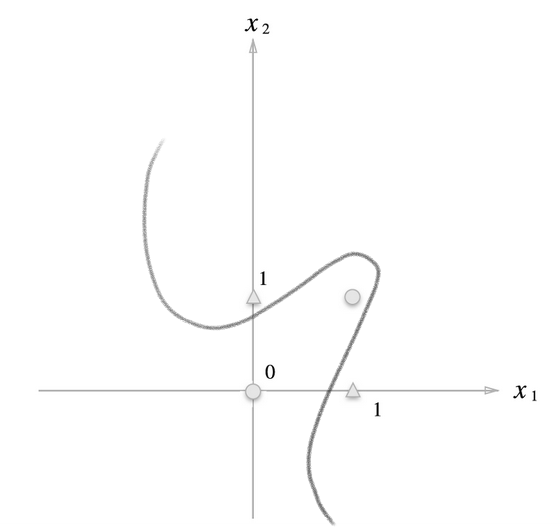
즉, 단일 퍼셉트론과 달리, 영역을 곡선으로 나눠서 분류할 수 있다는 의미입니다. 이는 위의 단일 퍼셉트론에서 XOR를 구현하지 못했던 문제점을 해결하며, 우리는 다층 퍼셉트론에서 XOR를 구현할 수 있게됩니다.
다층퍼셉트론은 입력 신호부터 출력 신호까지, 각각 0층, 1층, ..., n층으로 부릅니다. 이 퍼셉트론은 n층 퍼셉트론이라고 합니다. 하지만 문헌에 따라 1층부터 세어서, 1층, 2층, ... 으로 하는 경우도 있습니다.
ex) XOR 게이트를 2층 퍼셉트론으로 나타내보자

$y = (~(x_1*x_2))(x_1+x_2)$
XOR 게이트는 AND, NAND, OR 게이트를 조합하여 만들 수 있습니다. 같은 원리로, 2층 퍼셉트론을 잘 조합하면 복잡한 모델도 만들 수 있다는 것을 의미합니다.
이론상, 2층 퍼셉트론과 시그모이드(sigmoid) 활성화 함수를 이용하면, 임의의 함수를 모두 표현할 수 있다는 것이 증명되어 있습니다.
퍼셉트론과 신경망의 비교
퍼셉트론, 신경망 모두 여러 입력값을 받아서 하나의 입력값을 출력하는 공통점이 있습니다. 차이점으로는 퍼셉트론은 출력 값이 0 아니면 1이지만, 신경망은 다양한 출력 값을 가질 수 있습니다.
'Model > 인공신경망' 카테고리의 다른 글
| 경사 하강법을 이용한 신경망 학습 (0) | 2020.04.12 |
|---|---|
| Activation Function (활성화 함수) (0) | 2020.04.12 |
| 딥러닝 학습의 꽃, Backpropagation(역전파) (0) | 2020.04.12 |
| 인공신경망 (0) | 2020.04.12 |


