오늘은 Backpropagation에 대해서 알아보도록 하겠습니다. Backpropagation은 딥러닝에서 학습이 되는 과정을 이해하기에 꼭 필수적인 요소입니다. 우선, 계산 그래프와 연쇄 법칙에 대해 알아보겠습니다.
딥러닝 모델의 학습은 활성화 함수 값을 최소화하도록 학습합니다. 이는 순전파와 역전파를 반복하여 학습합니다.
- 순전파(feed forward): 입력값을 넣어 출력값을 계산하고, Loss function의 값을 구합니다.
- 역전파(Bacopropagation): 딥러닝 모델의 파라미터마다 편미분을 해서 Loss function 값이 최소화가 되도록 조절합니다.
Loss function에서 각각의 파라미터(가중치)마다 편미분을 하면 파라미터값을 얼마나 바꿔야 loss function이 감소하는지 알 수 있습니다. 수치미분법을 이용해 편미분을 하면 됩니다.

하지만 딥러닝 모델은 파라미터수가 매우 많으므로 모든 파라미터에 대해서 편미분을 수행하면 연산량 또한 매우 많아지게 됩니다. 이는 학습 시간이 늘어나게 하는 요인이 됩니다. 연산량을 줄이기 위한 방법으로 우리는 계산 그래프를 이용할 수 있습니다.
계산 그래프
계산 그래프란 계산 과정을 노드와 화살표로 표현하는 그래프를 일컫습니다.
계산 그래프는 전체가 복잡해도 각 노드에서 단순한 계산에 집중하여 문제를 단순화할 수 있습니다(국소적 계산). 또한 중간 계산 결과를 저장할 수 있고 역전파(backpropergation)를 통해 수치미분법보다 더 효율적으로 계산할 수 있습니다.
계산 그래프의 노드는 국소적 계산으로 구성되며, 국소적 계산을 조합해 전체 계산을 구성합니다. 계산 그래프의 순전파를 이용해 통상의 계산을 수행하며, 계산 그래프의 역전파를 이용해 각 노드의 미분을 구할 수 있습니다.
연쇄 법칙
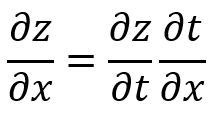
합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있습니다.
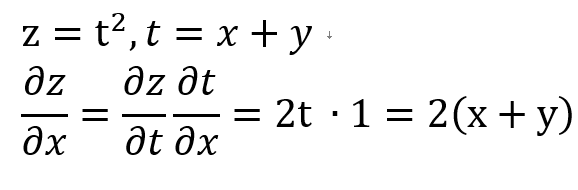
연쇄 법칙을 이용하여 t에 대한 z의 미분, x에 대한 t의 미분의 곱을 이용해 z에 대한 x의 미분을 나타낼 수 있습니다.
연쇄 법칙을 이용한 역전파
덧셈일 경우 z = x + y의 미분은 x에 대해 미분해도 1, y에 대해 미분해도 1입니다. 따라서 덧셈 노드의 역전파는 입력 값을 그대로 흘려보냅니다.
곱셈일 경우 z = xy의 미분은 x에 대해 미분하면 y, y에 대해 미분하면 x입니다.

활성화 함수의 역전파
순전파를 상류에서 하류로 값을 보낸다고 비유를 한다면, 활성화 함수의 역전파는 하류에서 들어온 값에 미분값을 곱한 값을 상류로 보냅니다.
활성화 함수에는 ReLu, Sigmoid와 같이 여러 종류가 있습니다. 이는 각각의 생김새에 따라 특성이 다르므로 적재적시에 사용할 수 있어야 합니다. 여기에서는 활성화 함수에 대해서는 기본적으로 알고 있다고 가정을 하고, 활성화 함수의 역전파에 대해 알아보도록 하겠습니다.
(활성화 함수에 대해 더 자세하게 알고 싶다면 아래 링크를 참고 부탁드립니다.)
Activation Function (활성화 함수)
Activation Function이란, 신경망의 출력값을 비선형적으로 변형시키는 역할을 합니다. 신경망의 출력이 선형(Linear)이라면 여러 층으로 쌓은 신경망을 단층 신경망으로 줄일 수 있습니다. 신경망 하
22-22.tistory.com
ReLu

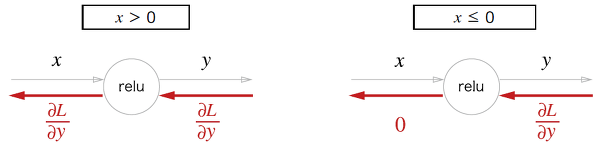
순전파 때의 입력인 x가 0보다 크면 상류의 값을 그대로 하류로 흘려 보냅니다. x가 0 이하이면 역전파 때는 하류로 신호를 보내지 않습니다.
Sigmoid
$\frac{1}{1 + exp(-x))^2} \times exp(-x) = y(1-y)$

따라서 순전파의 값 y만을 이용해, 순전파 값에 y(1-y)를 곱해서 하류로 신호를 보냅니다.
Affine 계층
affine transformation(어파인 변환)은 신경망의 순전파 때 수행하는 행렬의 곱을 의미합니다.
$Y = X * W + B $
위 그래프의 역전파 식은 아래와 같습니다.
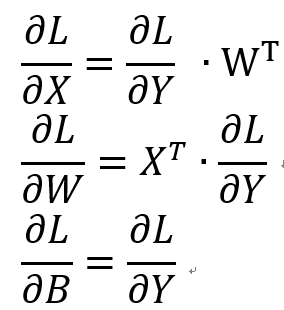
X, W, B 행렬 중에서 W, B는 내부에서 사용하는 파라미터입니다. X만이 입력값이므로 역전파 값은 dX 값만 반환하도록 구현합니다.
softmax-with-Loss
softmax layer를 통과한 뒤 cross-entropy-error를 계산하는 계층입니다.
역전파 값은 (모델 출력값) - (label 값)입니다. 따라서 모델 출력과 label이 일치하면 1, 완전 불일치하면 0입니다. 불일치하는 정도가 클수록 역전파 값의 절대값이 커져 파라미터가 학습되는 정도가 커지게 됩니다. 또한 cross entropy를 이용했기 때문에 역전파 값이 위와 같이 간단하게 나오게 됩니다. 마찬가지로 항등 함수와 MSE loss를 이용해도 이와 같은 값이 나오게 됩니다.
구현
Backpropagation은 수치 미분과 결과가 동일합니다. Backpropagation이 수치 미분보다 속도가 빠르지만 구현이 까다롭습니다. 따라서 수치미분을 이용한 값과 비교하면 오차역전파법이 제대로 구현되었는지 확인이 가능합니다.
참고자료
- 밑바닥부터 시작하는 딥러닝
- 오차 역전파 (backpropagation) - ratsgo's blog
'Model > 인공신경망' 카테고리의 다른 글
| 경사 하강법을 이용한 신경망 학습 (0) | 2020.04.12 |
|---|---|
| Activation Function (활성화 함수) (0) | 2020.04.12 |
| 뉴럴네트워크의 기본, 퍼셉트론(perceptron)에 대해 알아보자 (0) | 2020.04.12 |
| 인공신경망 (0) | 2020.04.12 |


